
登山によって消費されるカロリー(エネルギー)はどれくらいなのか。
それを知ることで登山中に補給すべきエネルギー量がわかります。補給しすぎると脂肪に変わり、補給しなさすぎるとシャリバテとなるということです。
補給しすぎは別にいいとは思いますが、補給しなさすぎると血糖値が下がって体に力が入らなくなり、行動不能になり、注意力の散漫や判断力の低下により事故を引き起こす可能性があるので、なるべくなら避けたいものです。
と考える人がいるのかどうか…。
多くの人は、登山によってどれだけ脂肪が落ちるのかが気になるのでは。
そう、どれだけダイエットできるのかが気になる人がこのページを読んでいる?
一般的には、METs法や山本教授が考案した公式によって計算すれば、簡単に消費カロリーの計算ができます。
でも、高校のときに習った物理学の力学的エネルギーがどうしても気になるので少し調べてみました。
行動中に必要となるエネルギー補給の参考になると思うので、備忘録としてまとめておきます。
ただし、素人が調べたものです。確実な情報源とはなりませんので、参考程度にしてください。
また、最後に山本教授が考案した式に基づき、体重などを入力すれば自動で計算してくれるフォームを掲載していますので使ってみてください。
METs(メッツ)法によるカロリー計算
METs(メッツ)とは、何かしらの動作や運動が安静状態に比べて何倍のエネルギーを使うかを示す単位です。安静時の消費カロリーを 1.0 として各種活動の消費カロリーが何倍になるかを示しています。
そのメッツ値は、国立健康・栄養研究所による『身体活動のメッツ(METs)表』で確認することができます。
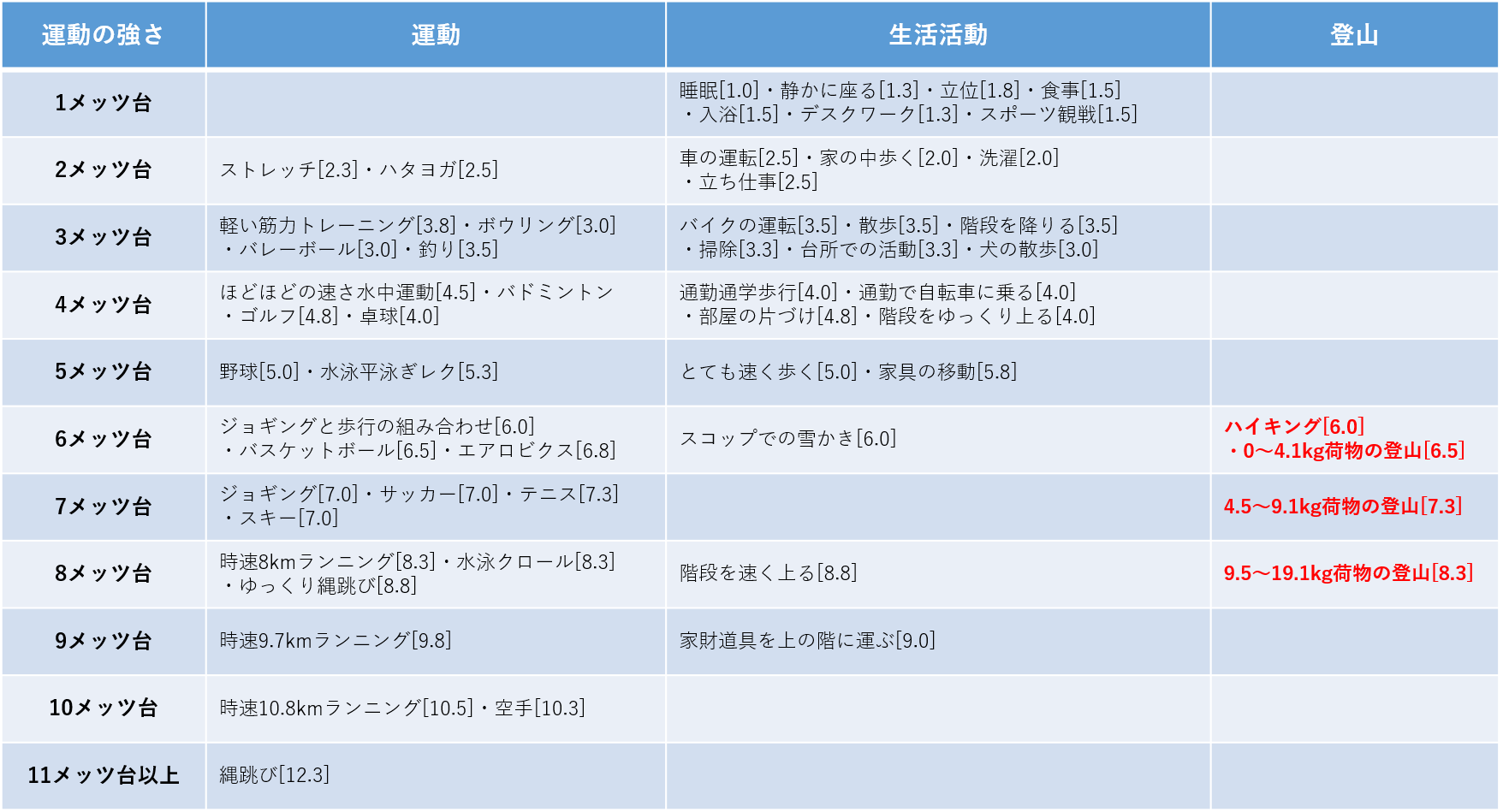
4.1kgまでの荷物での登山でも6.5メッツあるので、登山の運動強度は高いですね。バスケットボールするのと同じくらいの強度があります。安静状態に比べて6.5倍のエネルギーが必要になるということです。
テント泊縦走登山だと9.5~19.1kg のザック重量でしょうから、8.3メッツです。ということは、普段のトレーニングとして時速8kmランニングが必要であることがわかります。
そのメッツ値を用いた消費カロリーの計算式は、厚生労働省が作成する生活習慣病予防のための資料などに採用されている計算方式で次のとおりとなっています。
・消費カロリー(kcal) = 安静時の基礎代謝量 × メッツ × 運動時間
この「安静時の基礎代謝」については、簡易計算式では「体重 × 1.05」として計算するので、簡易計算式による式は
・消費カロリー(kcal) = (体重 × 1.05)× メッツ × 運動時間
となります。
たとえば、60kgの人が10kgのザックを背負い、6時間歩行した場合の消費カロリーは、
・(60kg×1.05)×8.3×6.0≒3,140kcal
ザックの重量を加えるべきか悩むところですが、ザック重量でメッツ値が変わってくることを踏まえると、純粋に体重のみとしました。
この計算式を見ると、単純にザック重量だけでメッツ値が決まっている点が気になります。
同じ体重の人が同じ重さのザックを背負い、標高差があまりない山と標高差がかなりある山を同じ時間歩行した場合では、その効率が違うため消費カロリーが同じ結果となることは考えにくいです。
よって、これは簡易計算式ということもあるので、消費カロリー計算は別なものを使ったほうがいいと思われます。
ただ、メッツ(運動強度)の値は参考になると思います。先に述べましたが、9.5~19.1kgのザックを背負って登山を計画している場合は、同等の運動強度であるものを普段のトレーニングとして取り入れる必要があり、この場合だと時速8kmランニングが必要であることがわかります。
山本教授が考案した公式によるカロリー計算
山本正嘉教授は、登山コースの体力的なキツさを数値として客観的に求める公式を考案しました。
皆さんもご存知の「ルート定数」と呼ばれているもので、荷物を背負って山登りをしたとき、行動時間と歩行距離、登りの標高差、下りの標高差の4つにそれぞれ係数を掛けて合計したものです。
今では、様々な登山コースにこのルート定数が示されていて、そのコースが体力的にどれくらいのキツさなのかを客観的に判断することができます。
このルート定数に重さ(自分の体重とザック重量の合計)の要素を掛け合わせることで、そのコースを歩いたときのエネルギー消費量が分かります。
その「登山中の消費エネルギーを計算する式」は、次のとおりです。
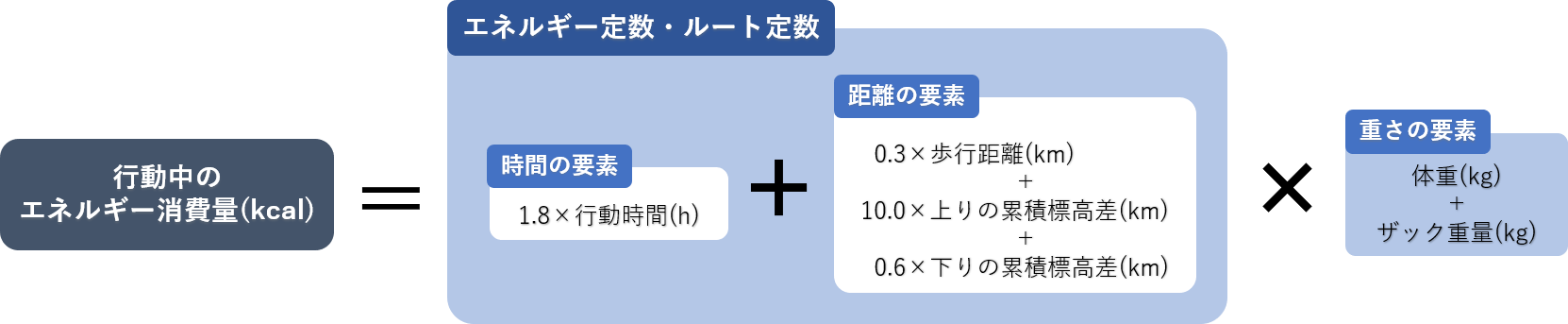
ここに、先ほどのMETs法により計算した事例と同じ条件で計算してみます。
60kgの人が10kgのザックを背負い、6時間歩行した場合のエネルギー消費量は、距離の要素となる歩行距離6.0km、上りの累積標高差1.18km、下りの累積標高差1.18kmを加えると、
・(1.8×6.0+(0.3×6.0+10.0×1.18+0.6×1.18))×(60+10)≒1,760kcal
となります。
METs法により導いた値よりかなり低い結果となります。
ただMETs法より距離の要素が加わっているので、こちらのほうがより詳細な数値と思われます。一般的には、この計算式で算出したものが登山における消費カロリーとして考えていいと思います。
物理学における力学的エネルギー
さて、ここで思い出すのは物理学の「力学的エネルギー」。
力学的エネルギーとは、物体を動かすのに必要なエネルギーで「運動エネルギー」と「位置エネルギー」を合わせたものです。
「運動エネルギー」とは、運動している物体がもつエネルギーで質量に比例し速さの二乗に比例します。つまり、物体の質量が大きいほど、また、速さが大きいほど大きなエネルギーを持っているということです。
「位置エネルギー」とは、その物体の位置のみによって決まるエネルギーで、物体の質量・高さ・重力加速度の積で得られます。つまり、物体のある場所が高ければ高いほどエネルギーを持っているということです。
高さ1,180mの場所にいる重さ70kgの人は
70(kg)×1,180(m)×9.8(m/s2)=809,480(J)
の位置エネルギーを持っているということです。
また、物体が2点間を移動するときに物体にはたらく力のする仕事が移動経路によらず一定である場合は力学的エネルギーの保存の法則が成り立ちます。
つまり、重さ70kgの人が高さ1,180mの場所に立つためには、809,480(J)のエネルギーを消費したということです。
ここで、物理では基本的に、エネルギーの単位は「ジュール(J)」を使います。
消費カロリーで「ジュール」と言われてもピンときません。やはり「カロリー」にしてもらわないとわからないですよね。
ジュールをカロリーに変換できる式があるのです。
それがこれ、
1cal = 4.2J 1J = 1/4.2 cal
となります。
よって、重さ70kgの人が高さ1,180mの場所に立ったときの消費カロリーは
809,480/4.2=192,733cal≒193kcal
となります。
たった193kcal?と思いますよね。
ここまでは物理学のお話で、ここからは生理学のお話。
人体は残念ながら消費するエネルギーは全て有効利用されるわけではなく、その多くは熱エネルギーに散逸してしまいます。
だいたい約2割しか有効利用されてなくて、残りの約8割は熱エネルギーになるといわれています。そのせいで運動すると汗が出るのです。
もし人体のエネルギー効率が100%だったら、いくら運動しても暑くなりません。
つまり、何が言いたいのかというと、
効率が20%しかない、ということは1カロリーの運動をするのに5カロリーぶんのエネルギーが消費されるということです。
というわけで、重さ70kgの人が高さ1,180mの場所に登った時に人体が消費するエネルギーは
193×5=965kcal
となります。
まあ、でも実際にはそんな単純な話ではないんでしょうね。
下山時のエネルギーや登山は登ったり下ったりの繰り返し。歩行も一定の前進速度で行われているようにみえますが、実際には、身体はステップごとにわずかに速度を早めたり遅めたりしています。
また、足さばきも静止から加速させてブレーキを両足が交互にしています。摩擦や風圧もあります。
当然これらもエネルギーを必要としているわけですから、単純ではないということがよく分かります。
そういった単純ではないものを客観的な数値として求める公式を導き出したのが、山本教授の式なのだと思います。つまり、山本教授が導き出した式によって得られるルート定数に自分の体重とザック重量を掛け合わしたエネルギー消費量が、客観的な数値といえます。
日本の主要な山の「ルート定数」は、検索すれば出てきます。
例えば、
・槍ヶ岳 上高地→槍ヶ岳→上高地 ルート定数70.3
・白馬岳 栂池自然園→白馬岳→栂池自然園 ルート定数42.8
です。
また、近所の低山でも累積標高差や距離、時間といった情報が検索するとあるので自分で導き出すことはできます。
なかなか面白いので、時間があるときに計算してみてくださいね。下に自動計算フォームを載せておきます。
以上で終わりま~す。

